Начертательная геометрия: конспект лекций.

3. Прямая, лежащая в данной плоскости.

Прямая принадлежит плоскости Р в том случае, если любые две ее точки лежат в данной плоскости.

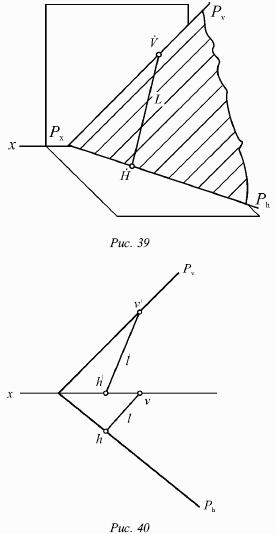
Например, если следы прямой лежат на одноименных следах плоскости, то прямая лежит в этой плоскости (рис. 39).

Рассмотрим построение прямой, лежащей в данной плоскости Р.

Первый способ. Возьмем на следах Р_h и Р_v по одной точке (рис. 40) и рассмотрим их как следы искомой прямой.

Рассматривая следы прямой, легко построить ее проекции.

Второй способ. Одну проекцию прямой, например горизонтальную 1, можно провести (рис. 40). Точки ее пересечения со следом Р_h и осью х определят горизонтальные проекции h и v следов искомой прямой. Если соединить прямой фронтальные проекции h́ и v́ следов, можно получить фронтальную проекцию 1́.